LOGIKA MATEMATIKA

Logika matematika adalah cabang logika dan matematika yang mengandung kajian matematis logika dan aplikasi kajian ini pada bidang-bidang lain di luar matematika. Logika matematika berhubungan erat dengan ilmu komputer dan logika filosofis. Tema utama dalam logika matematika antara lain adalah kekuatan ekspresif dari logika formal dan kekuatan deduktif dari sistem pembuktian formal. Logika matematika sering dibagi ke dalam cabang-cabang dari teori himpunan, teorimodel, teori rekursi, teoiri pembuktian, serta matematika konstruktif. Bidang-bidang ini memiliki hasil dasar logika yang serupa.

Hukum logika

1. Hukum komutatif
   • p ∧ q ≡ q ∧ p
   • p ∨ q ≡ q ∨ p
2. Hukum asosiatif
   • (p ∧ q) ∧ r ≡ p ∧ (q ∧ r)
   • (p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
3. Hukum distributif
   • p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
   • p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
4. Hukum identitas
   • p ∧ B ≡ p
   • p ∨ S ≡ p
5. Hukum ikatan
   • p ∧ S ≡ S
   • p ∨ B ≡ B
6. Hukum negasi
   • p ∧ ~p ≡ S
   • p ∨ ~p ≡ B
7. Hukum negasi ganda
   • ~(~p) ≡ p
8. Hukum idempotent
   • p ∧ p ≡ p
   • p ∨ p ≡ p
9. Hukum De Morgan
   • ~(p ∧ q) ≡ ~p ∨ ~q
   • ~(p ∨ q) ≡ ~p ∧ ~q
10. Hukum penyerapan
    • p ∧ (p ∨ q) ≡ p
    • p ∨ (p ∧ q) ≡ p
11. Negasi B dan S
    • ~B ≡ S
    • ~S ≡ B

Konjungsi, Disjungsi, Implikasi, dan Biimplikasi

Konjungsi merupakan operasi logika matematika dengan tanda hubung “dan”. Simbolnya adalah .
Jika ada dua pernyataan P dan Q, maka pada tabel kebenaran, hasilnya akan benar jika kedua pernyataannya bernilai benar. Sisanya salah.

Disjungsi merupakan logika matematika dengan tanda hubung “atau”, simbolnya .
Pada tabel kebenaran, hasilnya hanya salah jika kedua pernyataannya salah.

Implikasi disebut juga dengan “pernyataan bersyarat“, simbolnya adalah  atau , yang dibaca dengan “jika”. Misal  maka dibaca “jika P maka Q. Pada tabel kebenaran, hasilnya benar jika kedua pernyataannya benar atau kedua pernyataannya salah.

Biimplikasi merupakan implikasi dua arah, dengan simbol  atau 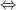. Misal , maka dibaca “P jika dan hanya jika Q”.

Pernyataan Majemuk

Pernyataan majemuk merupakan pernyataan yang terdiri dari beberapa pernyataan tunggal. Jadi, pernyataan ini terdiri dari beberapa operasi logika matematika.

Contoh: 

Konvers, Invers, dan Kontraposisi

Jika diketahui operasi logika matematika , maka berlaku:

Konvers: 

Invers:  

Kontraposisi: 

Pernyataan Berkuantor

Kuantor Universal atau kuantor umum, menggunakan kata: semua, seluruhnya, atau setiap. Contoh: Semua manusia akan mati. Simbolnya adalah 

Kuantor Eksistensial atau kuantor khusus, menggunakan kata: ada, beberapa, sebagian, terdapat. Contoh: Ada burung yang tidak bisa terbang. Simbolnya adalah .

Penarikan Kesimpulan

Dari beberapa pernyataan yang benar (premis) dan saling berhubungan, dapat ditarik suatu kesimpulan dari premis-premis tersebut.

Ada 3 pola utama dalam menarik suatu kesimpulan, yaitu modus ponens, modus tollens, dan silogisme.

Perhatikan pola berikut.

Teorema Sifat Aljabar Dalam Analisa Real

TEOREMA-TEOREMA PADA SIFAT ALJABAR ANALISA REAL

Teorema 1

Jika z∈ R ⋀ a∈ R lainnya yang bersifat z + a = a maka z = 0

Bukti 1 :

z + a = a, ∀a,z ∈ R ⇾ z = 0  

Akan dibuktikan 

Misal :

a,z ∈ R

z + a = a

Karena a∈R maka ∃(-a)∈ R ∋ a + (-a) = (-a) + a = 0

z + a + (-a) = a + (-a)

a + (z + (-a)) = a + (-a)             (Sifat asosiatif operaasi penjumlahan)

z + 0 = 0                                   (Sifat eksistensi elemen negatif)

z = 0                                         (Sifat kewujudan elemen nol)

∴ Jadi terbukti jika z ∈ R ⋀ a ∈ R lainnya yang bersifat z + a = a maka z = 0   

Bukti 2 :

Akan dibuktikan z + a = a, ∀a,z ∈ R ⇾ z = 0  

Misal :

a,z ∈ R

z + a = a

Berdasarkan sifat kewujudan elemen nol ∀z ∈ R

z = z + 0 

Berdasarkan sifat eksistensi elemen negatif

∃(-a)∈ R ∋ a + (-a) = (-a) + a = 0

Sehingga

z = z + (a + (-a))

z = (z + a) + a)

z = a = (-a)

z = 0

∴ Jadi terbukti jika z ∈ R ⋀ a ∈ R lainnya yang bersifat z + a = a maka z = 0

Teorema 2

Jika u ∈ R ⋀ b ≠ 0 ∈ R yang bersifat u,b = b, maka berlaku u = 1   

Bukti :

u,b = b,∀u,b ∈ R ⇾ b ≠ 0

Misal :

u,b ∈ R

u + b = b

Karena b∈ R ⋀ b ≠ 0  

Maka

∀a ∈ R, a ≠ 0,∃1a ∈ R ∋ 1a.a=a.1a=1

u * b = b

u * b.1b=b.1b                     (eksistensi elemen invers)

u * 1 = 1                             (aksioma kesatuan)

u = 1                                   (sifat kewujudan elemen satuan) 

∴ Jadi terbukti jika u ∈ R ⋀ b ≠ 0 ∈ R yang bersifat u,b = b, maka berlaku u = 1

Teorema 3

Jika a suatu elemen pada bilangan real, maka berlaku a.0 = 0 

Bukti :

a.0 = 0 ⇾ ∈ R

Karena a + a.0 = a.1 + a.0 = a.(1+0) = a.1 = a maka a.0 = 0 

Teorema 4

Jika a + b = 0, maka b = -a
Bukti:

Karena a + b = 0

a + b = 0 ↔ (-a) + (a + b) = (-a) + 0    

↔ ((-a) + a) + b = -a                            (sifat asosiatif penjumlahan dan eksistensi elemen nol)

↔ 0 + b = -a                                        (invers penjumlahan)

↔ b = -a                                              (eksistensi elemen nol)

 Teorema 5

Jika a ≠ 0 dan b ∈ R sedemikian hingga a . b = 1, maka b=1a

Bukti:

Karena a . b = 1, maka

a . b = 1 ↔ (1a)(a.b)=1a.1  

↔  (1a.a)(b)=1a 

↔  1.b=1a

↔  b=1a

Teorema 6

Jika a . b = 0, maka a = 0 atau b = 0

Bukti:

Diketahui a . b = 0, maka

a . b = 0 ↔ (1a)(a.b)=1a.0  

↔  (1a.a)(b)=0 

↔  1.b=0

↔  b=0

a . b = 0 ↔ (1b)(a.b)=1b.0  

↔  (1b.b)(a)=0 

↔  1.a=0

↔  a=0

Aljabar Dalam Kehidupan Sehari-hari

FUNGSI ALJABAR DALAM KEHIDUPAN SEHARI-HARI

Membahas mengenai manfaat Aljabar dalam kehidupan sehari-hari, mengingatkan kita yang mungkin sebagai guru atau orang tua saat ada pertanyaan yang terlontar dari anak dengan wajah polosnya. “Apa manfaat Aljabar dalam kehidupan kita sehari-hari?” Mereka belum tahu betapa pentingnya Aljabar yang merupakan dasar dari segala ilmu Matematika. Mungkin saat belajar Matematika di Sekolah Dasar kelas 1 atau 2 kita akan diberi soal seperti ini, “2 + Berapa? = 5”, bukankah itu serupa dengan “2 + x = 5, berapakah nilai x?” Setelah kita hitung maka akan menemukan jawabannya, yaitu 3. Selanjutnya, manfaat belajar Aljabar untuk kehidupan kita sehari-hari akan dikupas sebagai berikut.

1.      Penerapan Aljabar bagi siswa

Tentu saja, manfaat Aljabar bagi para pelajar adalah agar nilai ulangan Matematika tidak jatuh saat diberi soal Aljabar. Dan sebagai tambahan nilai untuk nilai kelulusan.

Selain itu, manfaat Aljabar yang sering diterapkan siswa adalah untuk memanajemen uang saku yang diberikan orang tua tiap minggu. Contoh penerapan aljabar dalam hal ini sebagai berikut:

Misalnya, uang saku kita sebesar Rp 70.000,00 setiap minggu. Karena setiap hari Selasa dan Rabu ada pelajaran tambahan, serta hari Jumat ada kegiatan ekstra kurikuler pada pukul 14.20 WIB sedangkan setelah pulang sekolah kita tidak pulang dahulu (langsung lanjut belajar tambahan) maka dibutuhkan uang makan + uang jajan sebesar Rp 10.000,00. Nah, kita kebingungan menentukan uang saku setiap hari selain Selasa, Rabu, dan Jum’at selama satu minggu jika dalam satu minggu itu kita ingin menabung uang sebesar Rp 25.000,00. Dengan bantuan aljabar kita dapat menentukan uang saku kita per hari.

Cara mengerjakan menggunakan Aljabar:

Kita anggap uang saku kita per hari (selain Selasa, Rabu, dan Jumat karena sudah ada jatahnya, yaitu Rp 10.000,00) dengan x. Maka,

Rp 70.000 = (uang saku 1 minggu)

Rp 25.000 = (uang tabungan selama 1 minggu)

70.000 – 25.000 = (3 X 10.000) + 1(6x -3x)

Rp 45.000 = Rp 30.000 + 1(3x)

Rp 45.000 = Rp 30.000 + 3x

Rp 45.000 – Rp 30.000 = 3x

Rp 15.000 = 3x

x = Rp 15.000/3

x = Rp 5.000

{Mengapa (3 X 10.000)? 3 berasal dari Hari Selasa, Rabu, dan Jumat dalam satu Minggu. Berarti kan ada 3 hari}

{Mengapa 1(6x – 3x)? 1 berasal dari 1 minggu sedangkan 6x – 3x berasal dari 6 hari dalam satu Minggu kecuali Minggu karena libur, dikurangi 3 hari (Selasa, Rabu, dan Jumat karena telah dijatah)}

Jadi, uang saku per hari yang kita gunakan selain Selasa, Rabu, dan Jumat (sekali lagi karena telah dijatah) dan selain Minggu (karena libur) maksimal sebesar Rp 5.000,00. Tidak boleh lebih tetapi boleh kurang (hehe, sebagai tambahan tabungan). Boleh lebih tetapi harus konsekuen, yaitu mengurangi jatah uang saku di hari berikutnya. Intinya silakan diatur sendiri ya uang saku dari ortu, latihan jadi menteri keuangan untuk diri sendiri.

2.      Penerapan Aljabar bagi Ibu Rumah Tangga

Manfaat aplikasi Aljabar bagi Ibu Rumah Tangga adalah untuk memanajemen uang gaji, uang saku anak, uang sekolah anak, dll. Contoh memanajemen uang bagi Ibu Rumah Tangga adalah sebagai berikut:

Seorang Ibu setiap bulan mendapat gaji sebesar Rp 2.000.000,00. Ia diberi uang tambahan dari suaminya sebesar Rp 4.000.000,00 per bulan. Dibutuhkan Rp 1.000.000,00 untuk uang belanja per bulan. Uang kesehatan Rp 500.000,00 dan uang sekolah total dari ke-2 anaknya sebesar Rp 3.000.000,00. Sang Ibu bingung, berapa uang saku perorangan yang harus ia berikan untuk kedua anaknya tiap minggu tetapi uang per bulannya harus masih tersisa Rp 1.000.000,00 untuk ditabung. Jika Ibu itu pintar Aljabar maka Ibu itu dapat menentukan uang saku tersebut secara tepat, tapi jika tidak? Hemm… silakan dibayangkan sendiri sesuai imajinasi masing-masing ya…

Cara mengerjakan menggunakan Aljabar:

Kita anggap uang saku setiap anak per minggu sebagai x

(2.000.000 + 4.000.000) – 1.000.000 = 1.000.000 + 500.000 + 3.000.000 + (4 X 2x)

6.000.000 – 1.000.000 = 4.500.000 + (8x)

5.000.000 = 4.500.000 + 8x

5.000.000 – 4.500.000 = 8x

500.000 = 8x

x = 500.000/8

x = 62.500

{Mengapa (4 X 2x) karena 1 bulan = 4 minggu dan 2x itu adalah uang saku 2 orang anak}.

Jadi, uang saku setiap anak dalam waktu seminggu adalah Rp 62.500,00. Dengan matematika dan sistem Aljabar, cukup simple kan?

3.      Penerapan Aljabar bagi para Pedagang.

Aljabar dapat membantu pedagang untuk menghitung besar kecil keuntungan atau kerugian yang dapat diperolehnya, dan dapat menentukan besar modal yang dibutuhkan. Contoh penerapan Aljabar dalam kehidupan pedagang adalah sebagai berikut:

Seorang pedagang pempek membeli 5 kg ikan giling dengan harga Rp 60.000,00. Dengan 5 kg ikan giling tersebut dapat dibuat menjadi 10 buah pempek kapal selam. Pedagang itu ingin laba tiap pempek tersebut sebesar Rp 2.000,00. Maka berapa harga jualnya? Jika pedagang itu pandai Matematika, pasti akan mudah mengetahuinya, sebaliknya, jika tidak, apa yang akan terjadi? Bisa dibayangkan sendiri segala kemungkinan yang akan terjadi dalam angan masing-masing…

Cara mengerjakan menggunakan sistem Aljabar:

Kita anggap harga jual pempek itu sebagai x.

Maka diperoleh:

x = (60.000/10) + 2.000

x = 6.000 + 2.000

x = 8.000

Jadi, harga jual yang bisa diterapkan agar laba satu pempek Rp 2.000 adalah sebesar Rp 8.000,00. Dengan Matematika dan aplikasi Aljabar, sangat simple kan?

Selamat belajar dan lebih mengakrabkan diri dengan Matematika. Make Mathematics part of our life. Karena Matematika adalah bagian sangat dekat yang tak terpisahkan dari kehidupan kita, salah satunya melalui pengaplikasian Aljabar dalam kehidupan sehari-hari.

Psikologi Pendidikan

Pengertian Psikologi Pendidikan

            Halo calon Pemimpin Bangsa disini saya akan menjelaskan tentang Psikologi Pendidikan semoga Bermanfaat !

Psikologi Pendidikan adalah ilmu yang mempelajari bagaimana manusia belajar dalam pendidikan pengaturan, efektivitas intervensi pendidikan, psikologi pengajaran, dan psikologi sosial dari sekolah sebagai organisasi. Psikologi pendidikan berkaitan dengan bagaimana siswa belajar dan berkembang, dan sering terfokus pada sub kelompok seperti berbakat anak-anak dan mereka yang tunduk pada khusus penyandang cacat .

Menurut Muhibin Syah (2002), pengertian psikologi pendidikan adalah sebuah disiplin psikologi yang menyelidiki masalah psikologis yang terjadi dalam dunia pendidikan. Sedangkan menurut  ensiklopedia amerika, Pengertian psikologi pendidikan adalah ilmu yang lebih berprinsip dalam proses pengajaran yang terlibat dengan penemuan – penemuan dan menerapkan prinsip – prinsip dan cara untuk meningkatkan keefisien di dalam pendidikan.Sedangkan menurut  Witherington, Pengertian Psikologi pendidikan adalah  studi sistematis tentang proses-proses dan faktor-faktor yang berhubungan dengan pendidikan manusia.

Tardif (dalam Syah, 1997: 13) juga mengatakan bahwa Pengertian Psikologi Pendidikan adalah sebuah bidang studi yang berhubungan dengan penerapan pengetahuan tentang perilaku manusia untuk usaha-usaha kependidikan.

Dari beberapa pendapat tentang psikologi pendidikan, kami mengambil kesimpulan bahwa Pengertian Psikologi Pendidikan adalah ilmu yang mempelajari  tentang perilaku manusia di dalam dunia pendidikan yang meliputi  studi sistematis tentang proses-proses dan faktor-faktor yang berhubungan dengan pendidikan manusia yang tujuannya untuk mengembangkan dan meningkatkan keefisien di dalam pendidikan.

Cara Cepat Mengerjakan Matematika

9 Cara Cepat Menghitung

            Halo Pemimpin Bangsa disini saya akan menjelaskan tentang cara cepat menghitung:

1. Menggunakan jarimu untuk menghitung perkalian 6,7,8,9.

Kalau mau menghitung jawaban dari 7x8, bisa menghitung dengan cara ini: 10 – 7 =3, jadi 3 jari di tangan kirimu adalah angka satuan, 2 jari di tangan kananmu juga adalah angka satuan. 2x3=6, jadi jawabannya untuk angka satuan adalah 6, jadi jari di bawah ditambahkan (2+3) adalah 5, jadi angka puluhan adalah 5. Jawabannya adalah 56.

2. Cara menghitung dalam hati dengan mudah.

3. Kelipatan 9 sangatlah teratur.

4. Pertambahan dan Perkalian dari Penyebut dan Pembilang

5. Bagaimana memecahkan 32x11.

6. Pi π＝3. 1415926, orang di luar negeri akan menghafalnya dengan :」May I Have A Large Container of Coffee」 caranya adalah dengan menghitung jumlah abjad per kata.

7. Menghitung Persentasi.Ketika kamu ingin menghitung 40%x300, kamu bisa langsung menghitung 4x30 = 120. Hilangkan 1 angka 0 nya, dalam beberapa detik kamu sudah tahu jawabannya.

8. Hubungan antara Celcius dan Farenheit. Farenheit = Celcius x 1.8 + 32

9. Bagaimana membedakan lebih besar dari dan lebih kecil dari.